前言：贪心算法也是用来解决最优化问题，将一个问题分成子问题，在现在子问题最优解的时，选择当前看起来是最优的解，期望通过所做的局部最优选择来产生一个全局最优解。书中先从活动选择问题来引入贪心算法，分别采用动态规划方法和贪心算法进行分析。本篇笔记给出活动选择问题的详细分析过程，并给出详细的实现代码进行测试验证。关于贪心算法的详细分析过程，下次在讨论。

1、活动选择问题描述

　　  有一个需要使用每个资源的n个活动组成的集合S= {a₁，a₂，···，a_n }，资源每次只能由一个活动使用。每个活动a_i都有一个开始时间s_i和结束时间f_i，且 0≤s_i<f_i<∞ 。一旦被选择后，活动a_i就占据半开时间区间[s_i,f_i)。如果[s_i,f_i]和[s_j,f_j]互不重叠，则称a_i和a_j两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

从图中可以看出S中共有11个活动，最大的相互兼容的活动子集为:{a₁，a₄，a₈，a11，}和{a₂，a₄，a₉，a₁₁}。

2、动态规划解决过程

（1）活动选择问题的最优子结构

定义子问题解空间S_ij是S的子集，其中的每个获得都是互相兼容的。即每个活动都是在a_i结束之后开始，且在a_j开始之前结束。

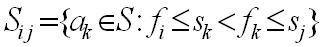
为了方便讨论和后面的计算，添加两个虚构活动a₀和a_n+1，其中f₀=0，s_n+1=∞。

结论：当i≥j时，S_ij为空集。

如果活动按照结束时间单调递增排序，子问题空间被用来从S_ij中选择最大兼容活动子集，其中0≤i＜j≤n+1，所以其他的S_ij都是空集。

最优子结构为：假设S_ij的最优解A_ij包含活动a_k，则对S_ik的解A_ik和S_kj的解A_kj必定是最优的。

通过一个活动a_k将问题分成两个子问题，下面的公式可以计算出S_ij的解A_ij。

（2）一个递归解

　　设c[i][j]为S_ij中最大兼容子集中的活动数目，当S_ij为空集时，c[i][j]=0；当S_ij非空时，若a_k在S_ij的最大兼容子集中被使用，则则问题S_ik和S_kj的最大兼容子集也被使用，故可得到c[i][j] = c[i][k]+c[k][j]+1。

当i≥j时，S_ij必定为空集，否则S_ij则需要根据上面提供的公式进行计算，如果找到一个a_k，则S_ij非空（此时满足f_i≤s_k且f_k≤s_j），找不到这样的a_k，则S_ij为空集。

c[i][j]的完整计算公式如下所示：

 

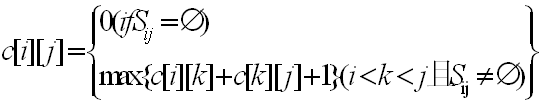
3、贪心算法解决过程

针对活动选择问题，认真分析可以得出以下定理：对于任意非空子问题S_ij，设a_m是S_ij中具有最早结束时间的活动，那么：

（1）活动a_m在S_ij中的某最大兼容活动子集中被使用。

（2）子问题S_im为空，所以选择am将使子问题S_mj为唯一可能非空的子问题。

有这个定理，就简化了问题，使得最优解中只使用一个子问题，在解决子问题S_ij时，在S_ij中选择最早结束时间的那个活动。

贪心算法自顶向下地解决每个问题，解决子问题S_ij，先找到S_ij中最早结束的活动a_m，然后将a_m添加到最优解活动集合中，再来解决子问题S_mj。

基于这种思想可以采用递归和迭代进行实现。递归实现过程如下所示：

void recursive_activity_selector(int *s,int* f,int i,int n,int *ret) { int *ptmp = ret; int m = i+1; //在Sin中寻找第一个结束的活动 while(m<=n && s[m] < f[i]) m = m+1; if(m<=n) { *ptmp++ = m; //添加到结果中 recursive_activity_selector(s,f,m,n,ptmp); } }

迭代实现过程如下：

void greedy_activity_selector(int *s,int *f,int *ret){  int i,m; *ret++ = 1; i =1; for(m=2;m<=N;m++) if(s[m] >= f[i]) { *ret++ = m; i=m; } }

完整C++代码：

#include
      
       using namespace std;const int N=11; int ret[11]={ 0}; static int num=0; void recursive_activity_selector(int *s,int *f,int i,int n) { int m=i+1; while(m<=n&&f[i]>s[m]) m=m+1; if(m<=n) { ret[num++]=m; recursive_activity_selector(s,f,m,n); } } void greedy_activity_selector(int *s,int *f,int i,int n) { int m=i+1; while(m<=n) { if(f[i]<=s[m]) { ret[num++]=m; i=m; } m++; } } int main() { int s[N+1] = {-1,1,3,0,5,3,5,6,8,8,2,12}; int f[N+1] = {-1,4,5,6,7,8,9,10,11,12,13,14}; int i; recursive_activity_selector(s,f,0,N); cout<<"最大子集为: "<
      

运行结果：